算法基础 本博客主要参照GitHub开源算法书籍hello-alo 以及oi-wiki ,这里对开源作者respect,感谢开源作者们的辛勤付出。
算法引入 算法其实在生活中无处不在,最典型的一个例子就是打扑克时对手牌洗牌。
将手牌分成两部分,左边为有序部分,右边为无序部分。然后让我们看看算法是怎么运行的(以78654为例且按升序排列)
最初有序部分为7,无序部分为8654 接着8>7,将8插入到7的右边,此时有序部分为78,无序部分为654 接着6<8,将8往右移,6<7,将7往左移,最后将6插在最左边 … 同理,像这样迭代,每次从无序部分取出最左边的元素,与有序部分里面的元素从右往左进行比较,找到属于自己的位置,最终得到升序的排序。 这就是插入排序 的思想。
什么是算法 通过上述的例子,想必大家对算法有了一个基本的了解。那么算法到底是什么?
输入特性:可以有零个输入,多个输入。 输出特性:必须要有输出。 有穷性:每个步骤都能在有限时间完成的。 确定性:对于每种情况下执行的操作,在算法中都有确定的规定,使算法的执行者或阅读者都能明确含义如何执行。 可行性:算法中所有操作必须足够基本都可以通过已经实现的操作运算有限次实现。 那么评估一个算法的优劣有哪些标准呢?
时间复杂度 和空间复杂度 是衡量一个算法效率的重要标准。
算法衡量标准 基本操作数 同一个算法在不同的计算机上运行的实际速度可能会不同,性能较好的计算机可能运行较快,于是用实际运算速度来评判一个算法的优劣显然是不妥的。所以通常考虑的不是算法的实际用时,而是算法运行所需要进行的基本操作的数量。
对基本操作的计数或是估测可以评判算法用时的指标。
基本操作数一般用T T T
渐进符号的定义 渐进符号是函数的阶的规范描述。简单来说,渐进符号忽略了一个函数中增长较慢的部分以及各项的系数(在时间复杂度相关分析中,系数一般被称作常数 ),而保留了可以用来表明该函数增长趋势的重要部分。
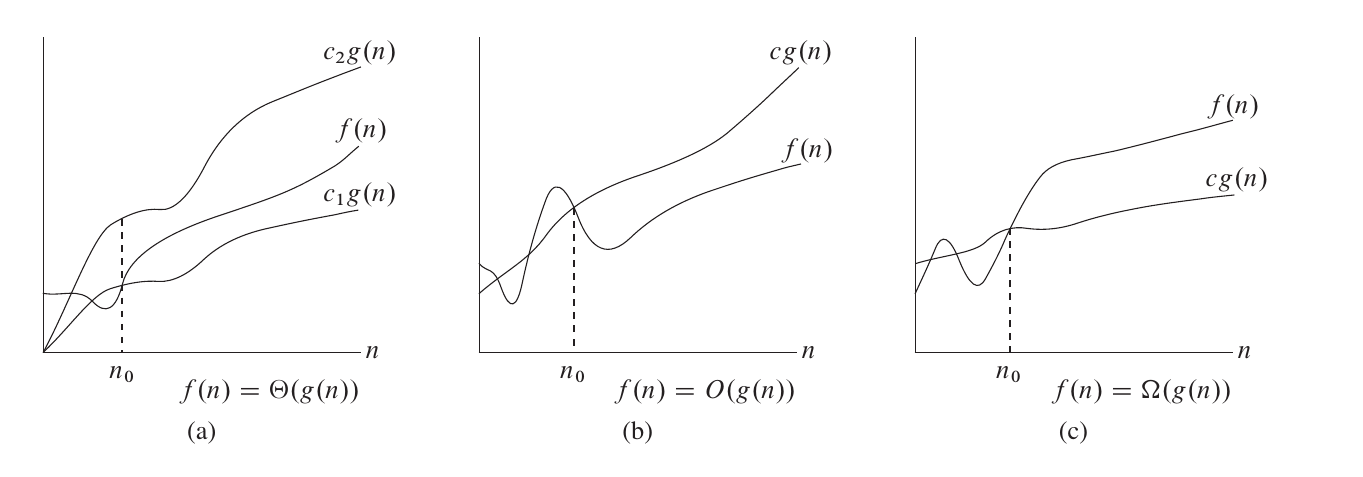
大Θ \Theta Θ 对于函数f ( n ) f(n) f ( n ) g ( n ) g(n) g ( n ) f ( n ) = Θ ( g ( n ) ) f(n)=\Theta(g(n)) f ( n ) = Θ ( g ( n ) ) ∃ c 1 , c 2 , n 0 > 0 \exists c_{1},c_{2},n_{0}>0 ∃ c 1 , c 2 , n 0 > 0 s . t . ∀ n ≥ n 0 s.t. \forall n\ge n_{0} s . t . ∀ n ≥ n 0 0 ≤ c 1 ∗ g ( n ) ≤ f ( n ) ≤ c 2 ∗ g ( n ) 0\le c_{1}*g(n)\le f(n)\le c_{2}*g(n) 0 ≤ c 1 ∗ g ( n ) ≤ f ( n ) ≤ c 2 ∗ g ( n )
看符号定义可能有点懵,主要思想就是找时间复杂度表达式里面谁占主导地位。
增长趋势为:$ln(x) < x^n < e^x $
例如 :3 n 2 + 5 n − 3 = Θ ( n 2 ) 3n^2+5n-3=\Theta(n^2) 3 n 2 + 5 n − 3 = Θ ( n 2 ) n 2 n^2 n 2 g ( n ) = n 2 g(n)=n^2 g ( n ) = n 2
严格按定义证明:
对于右侧:3 n 2 + 5 n − 3 < 3 n 2 + 5 n ≤ 3 n 2 + 5 n 2 = 8 n 2 3n^2+5n-3<3n^2+5n\le3n^2+5n^2=8n^2 3 n 2 + 5 n − 3 < 3 n 2 + 5 n ≤ 3 n 2 + 5 n 2 = 8 n 2
对于左侧:3 n 2 ≤ 3 n 2 + 5 n − 3 3n^2\le3n^2+5n-3 3 n 2 ≤ 3 n 2 + 5 n − 3
故显然c 1 c_{1} c 1 c 2 c_{2} c 2
大O O O Θ \Theta Θ O O O f ( n ) f(n) f ( n ) g ( n ) g(n) g ( n ) f ( n ) = O ( g ( n ) ) f(n)=O (g(n)) f ( n ) = O ( g ( n ) ) ∃ c , n 0 \exists c,n_{0} ∃ c , n 0 s . t . ∀ n ≥ n 0 s.t. \forall n\ge n_{0} s . t . ∀ n ≥ n 0 0 ≤ f ( n ) ≤ c ∗ g ( n ) 0\le f(n)\le c*g(n) 0 ≤ f ( n ) ≤ c ∗ g ( n )
研究时间复杂度通常会使用O O O
大Ω \Omega Ω 用Ω \Omega Ω f ( n ) f(n) f ( n ) g ( n ) g(n) g ( n ) f ( n ) = Ω ( g ( n ) ) f(n)=\Omega(g(n)) f ( n ) = Ω ( g ( n ) ) ∃ c , n 0 \exists c,n_{0} ∃ c , n 0 s . t . ∀ n ≥ n 0 s.t. \forall n\ge n_{0} s . t . ∀ n ≥ n 0 0 ≤ c ∗ g ( n ) ≤ f ( n ) 0\le c*g(n) \le f(n) 0 ≤ c ∗ g ( n ) ≤ f ( n )
小ο \omicron ο 学过高数的小伙伴可能一点也不陌生,高阶无穷小就是用ο \omicron ο ο \omicron ο O O O ο \omicron ο f ( n ) f(n) f ( n ) g ( n ) g(n) g ( n ) f ( n ) = ο ( g ( n ) ) f(n)=\omicron(g(n)) f ( n ) = ο ( g ( n ) ) ∃ c , n 0 \exists c,n_{0} ∃ c , n 0 s . t . ∀ n ≥ n 0 s.t. \forall n\ge n_{0} s . t . ∀ n ≥ n 0 0 ≤ f ( n ) < c ∗ g ( n ) 0\le f(n)< c*g(n) 0 ≤ f ( n ) < c ∗ g ( n )
小ω \omega ω 和O O O ο \omicron ο Ω \Omega Ω ≤ \le ≤ ω \omega ω
对于函数f ( n ) f(n) f ( n ) g ( n ) g(n) g ( n ) f ( n ) = ω ( g ( n ) ) f(n)=\omega(g(n)) f ( n ) = ω ( g ( n ) ) ∃ c , n 0 \exists c,n_{0} ∃ c , n 0 s . t . ∀ n ≥ n 0 s.t. \forall n\ge n_{0} s . t . ∀ n ≥ n 0 0 ≤ c ∗ g ( n ) ≤ f ( n ) 0\le c*g(n) \le f(n) 0 ≤ c ∗ g ( n ) ≤ f ( n )
这里oi-wiki 也放了几张图片供读者理解:
渐进符号的常见性质 f ( n ) = Θ ( g ( n ) ) ⟺ ( f ( n ) = O ( g ( n ) ) ) ∧ ( f ( n ) = Ω ( g ( n ) ) ) f(n)=\Theta(g(n))\Longleftrightarrow (f(n)=O(g(n)))\wedge(f(n)=\Omega(g(n))) f ( n ) = Θ ( g ( n ) ) ⟺ ( f ( n ) = O ( g ( n ) ) ) ∧ ( f ( n ) = Ω ( g ( n ) ) ) f ( x ) + g ( x ) = O ( m a x ( f ( x ) , g ( x ) ) ) f(x)+g(x)=O(max(f(x),g(x))) f ( x ) + g ( x ) = O ( m a x ( f ( x ) , g ( x ) ) ) f ( x ) ∗ g ( x ) = O ( f ( x ) ∗ g ( x ) ) f(x)*g(x)=O(f(x)*g(x)) f ( x ) ∗ g ( x ) = O ( f ( x ) ∗ g ( x ) ) ∀ a ≠ 1 \forall a\neq1 ∀ a = 1 log a n = O ( l o g 2 n ) \log_{a}n=O(log_{2}n) log a n = O ( l o g 2 n ) 常见阶的增长速度排序:
O ( 1 ) < O ( l o g n ) < O ( n ) < O ( n l o g n ) < O ( n 2 ) < O ( 2 n ) < O ( n ! ) O(1)<O(log n)<O(n)<O(nlogn)<O(n^2)<O(2^n)<O(n!) O ( 1 ) < O ( l o g n ) < O ( n ) < O ( n l o g n ) < O ( n 2 ) < O ( 2 n ) < O ( n ! )
时间复杂度 定义:
衡量一个算法的快慢,一定要考虑数据规模的大小。所谓数据规模,一般指输入的数字个数、输入中给出的图的点数与边数等等。一般来说,数据规模越大,算法的用时就越长。而在算法竞赛中,我们衡量一个算法的效率时,最重要的不是看它在某个数据规模下的用时,而是看它的用时随数据规模而增长的趋势,即 时间复杂度 。
这里的数据规模的增长趋势类似于数学里面的增长趋势,所谓「用时随数据规模而增长的趋势」是一个模糊的概念,需要借助上文所介绍的 渐进符号 来形式化地表示时间复杂度。
时间复杂度例子 非递归算法的时间复杂度 例一:
void algorithm_A (int n) cout << "hello world" << endl; }
基本操作只有一次打印hello world的操作,而与输入的参数n无关,所以时间复杂度是常数阶,即O ( 1 ) O(1) O ( 1 )
例二:
#include <iostream> using namespace std;int main () void algorithm (int n, int m) for (int i = 0 ;i < n; i++) { for (int j = 0 ;j < m; j++) { cout << "hello world" << endl; } } } }
要计算基本操作,主要就是看打印了hello world多少次,外循环n次,内循环m次,不难得出,总共操作了m*n次。所以时间复杂度就是O ( m ∗ n ) O(m*n) O ( m ∗ n )
例三:
void algorithm (int n) int a = 1 ; a = a + n; for (int i = 0 ; i < 5 * n ; i++) { cout << "hello world" << endl; } for (int i = 0 ; i < 2 * n; i++) { for (int j = 0 ; j < n ; j++) { cout << "hello world" << endl; } } }
这个算法主要分为三个部分:
综上所述:基本操作数总和为2 n 2 + 5 n + 2 2n^2+5n+2 2 n 2 + 5 n + 2 O O O O ( n 2 ) O(n^2) O ( n 2 )
例四:
void algorithm (int n) for (int i = 1 ; i <= n; i*=2 ) { cout << "hello world" << endl; } }
可以看到循环执行完之后,i的值变成了原来的2倍,呈指数增长。不妨设循环执行了k次,则i最后的值为2 k > n 2^k >n 2 k > n 2 k − 1 = n 2^{k-1}=n 2 k − 1 = n O ( l o g n ) O(logn) O ( l o g n )
例五:
void algorithm (int n) for (int i = 0 ; i < n; i++) { for (int j = 0 ; j <= i ; j++) { cout << "hello world" << endl; } } }
可以看到这种不同循环之间含有依赖的,可以用∑ \sum ∑
∑ i ∈ { 1 , 2 , . . . , n } ∑ j ∈ { 1 , 2 , . . . , i } 1 \sum_{\substack{i\in\{1,2,...,n\}}}\sum_{\substack{j\in\{1,2,...,i\}}}1 i ∈ { 1 , 2 , . . . , n } ∑ j ∈ { 1 , 2 , . . . , i } ∑ 1
然后再从里层循环向外层循环求和,如下
∑ i ∈ { 1 , 2 , . . . , n } ∑ j ∈ { 1 , 2 , . . . , i } 1 = ∑ i ∈ { 1 , 2 , . . . , n } i = n 2 + n 2 \sum_{\substack{i\in\{1,2,...,n\}}}\sum_{\substack{j\in\{1,2,...,i\}}}1=\sum_{\substack{i\in\{1,2,...,n\}}}i=\frac{n^2+n}{2} i ∈ { 1 , 2 , . . . , n } ∑ j ∈ { 1 , 2 , . . . , i } ∑ 1 = i ∈ { 1 , 2 , . . . , n } ∑ i = 2 n 2 + n
故时间复杂度为O ( n 2 ) O(n^2) O ( n 2 )
例六:
void algorithm (int n) for (int i = 1 ; i < n; i++) { for (int j = 1 ; j <= i ; j*=2 ) { cout << "hello world" << endl; } } }
同样设置内层循环执行了k次,简化有2 k − 1 = i 2^{k-1}=i 2 k − 1 = i
∑ i ∈ { 1 , 2 , . . . , n } ∑ j ∈ { 1 , 2 , . . . , i } 1 \sum_{\substack{i\in\{1,2,...,n\}}}\sum_{\substack{j\in\{1,2,...,i\}}}1 i ∈ { 1 , 2 , . . . , n } ∑ j ∈ { 1 , 2 , . . . , i } ∑ 1
求和有:
∑ i ∈ { 1 , 2 , . . . , n } ∑ j ∈ { 1 , 2 , 4 , . . . , 2 k − 1 } 1 = ∑ i ∈ { 1 , 2 , . . . , n } l o g i = O ( l o g 1 + l o g 2 + . . . + l o g n ) = O ( l o g ( n ! ) ) ≈ O ( n l o g n ) \sum_{\substack{i\in\{1,2,...,n\}}}\sum_{\substack{j\in\{1,2,4,...,2^{k-1}\}}}1=\sum_{\substack{i\in\{1,2,...,n\}}}log\ i=O(log\ 1+log\ 2+...+log\ n)=O(log\ (n!))\approx O(nlog\ n) i ∈ { 1 , 2 , . . . , n } ∑ j ∈ { 1 , 2 , 4 , . . . , 2 k − 1 } ∑ 1 = i ∈ { 1 , 2 , . . . , n } ∑ l o g i = O ( l o g 1 + l o g 2 + . . . + l o g n ) = O ( l o g ( n ! ) ) ≈ O ( n l o g n )
其中O ( l o g ( n ! ) ) ≈ O ( n l o g n ) O(log\ (n!))\approx O(nlog\ n) O ( l o g ( n ! ) ) ≈ O ( n l o g n ) 斯特林公式 :
n ! ≈ 2 π n ( n e ) n n!\approx \sqrt{2\pi n}(\frac{n}{e})^n n ! ≈ 2 π n ( e n ) n
来近似的
例七:
void algorithm (int n) for (int i = 1 ; i < n; i*=2 ) { for (int j = 1 ; j <= i ; j++) { cout << "hello world" << endl; } } }
和前面一样不多赘述,这里直接列出表达式
∑ i ∈ { 1 , 2 , . . . , 2 k − 1 } ∑ j ∈ { 1 , 2 , 3 , . . . , i } 1 = ∑ i ∈ { 1 , 2 , . . . , 2 k − 1 } i = O ( 1 + 2 + 4 + . . . + 2 k − 1 ) = O ( 2 k − 1 ) = O ( 2 n − 1 ) = O ( n ) \sum_{\substack{i\in\{1,2,...,2^{k-1}\}}}\sum_{\substack{j\in\{1,2,3,...,i\}}}1=\sum_{\substack{i\in\{1,2,...,2^{k-1}\}}}i=O(1+2+4+...+2^{k-1})=O(2^{k}-1)=O(2n-1)=O(n) i ∈ { 1 , 2 , . . . , 2 k − 1 } ∑ j ∈ { 1 , 2 , 3 , . . . , i } ∑ 1 = i ∈ { 1 , 2 , . . . , 2 k − 1 } ∑ i = O ( 1 + 2 + 4 + . . . + 2 k − 1 ) = O ( 2 k − 1 ) = O ( 2 n − 1 ) = O ( n )
递归算法的时间复杂度 例一:
比较经典的一个递归是汉诺塔 问题,这里直接给出通项:
\begin{equation} T(n) = \begin{cases} 1 & \text{if } n=1 \\ 2T(n-1)+O(1) & \text{if } n>1 \end{cases} \end{equation}
通过一直迭代的方法就可以求得时间复杂度:T ( n ) = 2 T ( n − 1 ) + O ( 1 ) = 2 ( 2 T ( n − 2 ) + O ( 1 ) ) + O ( 1 ) = . . . = 2 n T ( 1 ) − 1 T(n)=2T(n-1)+O(1)=2(2T(n-2)+O(1))+O(1)=...=2^{n}T(1)-1 T ( n ) = 2 T ( n − 1 ) + O ( 1 ) = 2 ( 2 T ( n − 2 ) + O ( 1 ) ) + O ( 1 ) = . . . = 2 n T ( 1 ) − 1
故时间复杂度为O ( 2 n ) O(2^n) O ( 2 n )
主定理(Master Theorem):
对于一个母问题n,可以将其分解为a a a n b \frac{n}{b} b n f ( n ) f(n) f ( n )
对于递推关系式:
T ( n ) = a T ( n b ) + f ( n ) T(n)=aT(\frac{n}{b})+f(n) T ( n ) = a T ( b n ) + f ( n )
用递归树来演示这个过程:
向下递归直到最后一行每一个子问题的时间复杂度为O ( 1 ) O(1) O ( 1 ) a h a^h a h n = b h n=b^h n = b h h = l o g b n h=log_{b}n h = l o g b n n l o g b a n^{log_{b}a} n l o g b a T ( n ) = Θ ( n l o g b a ) + g ( n ) T(n)=\Theta(n^{log_{b}a})+g(n) T ( n ) = Θ ( n l o g b a ) + g ( n ) g ( n ) g(n) g ( n )
结合渐进符号的定义,整体的T ( n ) T(n) T ( n )
f ( n ) = O ( n l o g b a − ϵ ) f(n)=O(n^{log_{b}a-\epsilon}) f ( n ) = O ( n l o g b a − ϵ ) ϵ \epsilon ϵ g ( n ) = O ( n l o g b a ) g(n)=O(n^{log_{b}a}) g ( n ) = O ( n l o g b a ) T ( n ) = Θ ( n l o g b a ) T(n)=\Theta(n^{log_{b}a}) T ( n ) = Θ ( n l o g b a ) 总结有以下定理:
\begin{equation} T(n) = \begin{cases} \Theta(n^{log_{b}a}) & \text{if } f(n)=O(n^{log_{b}(a)-\epsilon}),\epsilon>0 \\ \Theta(f(n)) & \text{if } f(n)=\Omega(n^{log_{b}(a)+\epsilon}),\epsilon \ge0 \\ \Theta(n^{log_{b}a}log^{k+1}n) & \text{if } f(n)=\Theta(n^{log_{b}a}log^{k}n),k\ge0 \end{cases} \end{equation}
最差、最佳、平均时间复杂度 算法的时间效率往往不是固定的,而是与输入数据的分布有关 。
例如如果想要在一个长度为n的数组找到某一特定的数x,由以下两种极端情况:
最佳情况:[x, ?, ?, … , ?],此时为最佳时间复杂度O ( 1 ) O(1) O ( 1 ) x],此时为最差时间复杂度O ( n ) O(n) O ( n )
最差时间复杂度”对应函数渐近上界,则使用O O O Ω \Omega Ω
实际情况中,最佳和最差时间复杂度出现的概率很小,相比之下,用平均时间复杂度可以体现算法在随机输入数据下的运行效率 ,用Θ \Theta Θ x出现在任意位置的概率相等,即为1 n \frac{1}{n} n 1
1 + 2 + 3 + 4 + . . . + n n = n 2 + n 2 n = n 2 + 1 2 \frac{1+2+3+4+...+n}{n}=\frac{n^2+n}{2n}=\frac{n}{2}+\frac{1}{2} n 1 + 2 + 3 + 4 + . . . + n = 2 n n 2 + n = 2 n + 2 1
分子的含义是x在数组中某个位置需要进行查找操作的数目之和,如3表示在x第三个位置需要查找三次。所以平均时间复杂度就为Θ ( n ) \Theta(n) Θ ( n )
空间复杂度 用于衡量算法占用内存空间随着数据量变大时的增长趋势。这个概念与时间复杂度非常类似,只需将“运行时间”替换为“占用内存空间”。
算法相关空间: __输入空间:__用于存储算法的输入数据 __暂存空间:__用于存储算法在运行时的变量、对象、函数上下文等数据,可以分为三部分: __暂存数据:__用于保存算法运行过程中的各种常量、变量、对象等。 __栈帧空间:__用于保存调用函数的上下文数据。系统在每次调用函数时都会在栈顶部创建一个栈帧,函数返回后,栈帧空间会被释放。 __指令空间:__用于保存编译后的程序指令,在实际统计中通常忽略不计。 __输出空间:__用于存储算法的输出数据 空间复杂度例子 实际计算中,通常只考虑最差空间复杂度 。因为运行程序时必须保证在所有输入数据下都要足够的内存空间预留。
非递归算法 void algorithm (int n) int a = 0 ; vector<int > b (10000 ) ; if (n > 10 ) vector<int > nums (n) ; }
用最差输入数据视角 来看最差空间复杂度:n < 10 n<10 n < 1 0 O ( 1 ) O(1) O ( 1 ) n > 10 n>10 n > 1 0 O ( n ) O(n) O ( n ) O ( n ) O(n) O ( n ) 用算法运行中的峰值内存 来看最差空间复杂度:运行到最后一行前,占用O ( 1 ) O(1) O ( 1 ) O ( n ) O(n) O ( n ) O ( n ) O(n) O ( n ) 递归算法 int func () return 0 ; } void loop (int n) for (int i = 0 ; i < n; i++) { func (); } } void recur (int n) if (n == 1 ) return ; return recur (n - 1 ); }
函数 loop() 在循环中调用了 n 次 function() ,每轮中的 function() 都返回并释放了栈帧空间,因此空间复杂度仍为O ( 1 ) O(1) O ( 1 ) 递归函数 recur() 在运行过程中会同时存在 n 个未返回的 recur() ,从而占用O ( n ) O(n) O ( n ) 权衡时间与空间 经常可以听到时间换空间 ,空间换时间 等术语,实际情况中,同时优化时间复杂度和空间复杂度通常非常困难。
在大多数情况下,时间比空间更宝贵,因此“以空间换时间”通常是更常用的策略。当然,在数据量很大的情况下,控制空间复杂度也非常重要。